Mittwoch, 27. April 2011
Beispiele zu Gleitkommadarstellung (POS1: 1B)
Hier finden Sie ein paar Übungsbeispiele zu Gleitkommazahlen sowie die dazugehörige Lösung. Zunächst Konvertierung von Dezimalzahlen in Gleitkommazahlen. Es sind die Zahlen immer alle drei Formate zu bestimmen:
-0,15087890625
33
470,171875
-17,2145
-0,015625
12739
Beide Vorzeichen positiv
Mantisse: 1111100002
positiver Exponent: 1012 = 510
Zahl in normierter Gleitkommadarstellung: 0,111112 * 25 = 111112
Ergebnis: 31
Vorzeichen der Mantisse negativ, daher ist die Zahl negativ
Mantisse: 1100101012
positiver Exponent: 1112 = 710
Zahl in normierter Gleitkommadarstellung: -0,1100101012 * 27 = 1100101,012
Ergebnis: -101,25
beide Vorzeichen negativ, daher ist die Zahl negativ und der Exponent negativ
negative Mantisse: -1001101012
negativer Exponent, daher Zweierkomplement des Exponenten: 0102 = -210
Zahl in normierter Gleitkommadarstellung: -0,1001101012 * 2-2 = 0,001001101012
Ergebnis: -0.15087890625
(Vergleichen Sie das mit dem Ergebnis des Beispiels ganz oben!)
-0,15087890625
Nachkommateil:
0.15087891 | 0
0.30175781 | 0
0.60351562 | 1
0.20703125 | 0
0.41406250 | 0
0.82812500 | 1
0.65625000 | 1
0.31250000 | 0
0.62500000 | 1
0.25000000 | 0
0.50000000 | 1
Gesamt: 1 ,00100110101 (die 1 steht für das Vorzeichen -)
Mantisse wäre: 1001101010
Exponent wäre: -2
Exponent umwandeln:
2 | 0
1 | 1
Exponent unbeschränkt positiv: 10
Exponent mit führenden Nullen: 0010
Zweierkomplement:
Einerkomplement: 1101
1
Zweierkomplement: 1110
Exponent: 1110, Vorzeichen: 1
vm m m m m m m m m m m ve e e e e
1 1 0 0 1 1 0 1 0 1 0 1 1 1 1 0
vm ve e e e e m m m m m m m m m m
1 1 1 1 1 0 1 0 0 1 1 0 1 0 1 0
ve e e e e vm m m m m m m m m m m
1 1 1 1 0 1 1 0 0 1 1 0 1 0 1 0
33
ganzzahliger Teil:
33 | 1
16 | 0
8 | 0
4 | 0
2 | 0
1 | 1
Nachkommateil:
Gesamt: 0 100001, (die 0 steht für das Vorzeichen + - beachte den Abstand)
Mantisse wäre: 1000010000
Exponent wäre: 6
Exponent umwandeln:
6 | 0
3 | 1
1 | 1
Exponent unbeschränkt positiv: 110
Exponent: 0110, Vorzeichen: 0
vm m m m m m m m m m m ve e e e e
0 1 0 0 0 0 1 0 0 0 0 0 0 1 1 0
vm ve e e e e m m m m m m m m m m
0 0 0 1 1 0 1 0 0 0 0 1 0 0 0 0
ve e e e e vm m m m m m m m m m m
0 0 1 1 0 0 1 0 0 0 0 1 0 0 0 0
470,171875
ganzzahliger Teil:
470 | 0
235 | 1
117 | 1
58 | 0
29 | 1
14 | 0
7 | 1
3 | 1
1 | 1
Nachkommateil:
0.17187500 | 0
0.34375000 | 0
0.68750000 | 1
0.37500000 | 0
0.75000000 | 1
0.50000000 | 1
Gesamt: 0 111010110,001011
Mantisse wäre: 1110101100
Exponent wäre: 9
Exponent umwandeln:
9 | 1
4 | 0
2 | 0
1 | 1
Exponent unbeschränkt positiv: 1001
Exponent: 1001, Vorzeichen: 0
vm m m m m m m m m m m ve e e e e
0 1 1 1 0 1 0 1 1 0 0 0 1 0 0 1
vm ve e e e e m m m m m m m m m m
0 0 1 0 0 1 1 1 1 0 1 0 1 1 0 0
ve e e e e vm m m m m m m m m m m
0 1 0 0 1 0 1 1 1 0 1 0 1 1 0 0
-17,2145
ganzzahliger Teil:
17 | 1
8 | 0
4 | 0
2 | 0
1 | 1
Nachkommateil:
0.21450000 | 0
0.42900000 | 0
0.85800000 | 1
0.71600000 | 1
0.43200000 | 0
0.86400000 | 1
0.72800000 | 1
0.45600000 | 0
0.91200000 | 1
0.82400000 | 1
0.64800000 | 1
0.29600000 | 0
0.59200000 | 1
0.18400000 | 0
0.36800000 | 0
0.73600000 | 1
0.47200000 | 0
0.94400000 | 1
Gesamt: 1 10001,001101101110100101
Mantisse wäre: 1000100110
Exponent wäre: 5
Exponent umwandeln:
5 | 1
2 | 0
1 | 1
Exponent unbeschränkt positiv: 101
Exponent: 0101, Vorzeichen: 0
vm m m m m m m m m m m ve e e e e
1 1 0 0 0 1 0 0 1 1 0 0 0 1 0 1
vm ve e e e e m m m m m m m m m m
1 0 0 1 0 1 1 0 0 0 1 0 0 1 1 0
ve e e e e vm m m m m m m m m m m
0 0 1 0 1 1 1 0 0 0 1 0 0 1 1 0
-0,015625
ganzzahliger Teil:
Nachkommateil:
0.01562500 | 0
0.03125000 | 0
0.06250000 | 0
0.12500000 | 0
0.25000000 | 0
0.50000000 | 1
Gesamt: 1 ,000001
Mantisse wäre: 1000000000
Exponent wäre: -5
Exponent umwandeln:
5 | 1
2 | 0
1 | 1
Exponent unbeschränkt positiv: 101
Exponent mit führenden Nullen: 0101
Zweierkomplement:
Einerkomplement: 1010
1
Zweierkomplement: 1011
Exponent: 1011, Vorzeichen: 1
vm m m m m m m m m m m ve e e e e
1 1 0 0 0 0 0 0 0 0 0 1 1 0 1 1
vm ve e e e e m m m m m m m m m m
1 1 1 0 1 1 1 0 0 0 0 0 0 0 0 0
ve e e e e vm m m m m m m m m m m
1 1 0 1 1 1 1 0 0 0 0 0 0 0 0 0
12739
ganzzahliger Teil:
12739 | 1
6369 | 1
3184 | 0
1592 | 0
796 | 0
398 | 0
199 | 1
99 | 1
49 | 1
24 | 0
12 | 0
6 | 0
3 | 1
1 | 1
Nachkommateil:
Gesamt: 0 11000111000011,
Mantisse wäre: 1100011100
Exponent wäre: 14
Exponent umwandeln:
14 | 0
7 | 1
3 | 1
1 | 1
Exponent unbeschränkt positiv: 1110
Exponent: 1110, Vorzeichen: 0
vm m m m m m m m m m m ve e e e e
0 1 1 0 0 0 1 1 1 0 0 0 1 1 1 0
vm ve e e e e m m m m m m m m m m
0 0 1 1 1 0 1 1 0 0 0 1 1 1 0 0
ve e e e e vm m m m m m m m m m m
0 1 1 1 0 0 1 1 0 0 0 1 1 1 0 0
Zurückrechnen
Gegeben sind die Zahlen im 2. Format, m = 9 und e = 3:0 0 1 0 1 1 1 1 1 1 0 0 0 0Beide Vorzeichen positiv
Mantisse: 1111100002
positiver Exponent: 1012 = 510
Zahl in normierter Gleitkommadarstellung: 0,111112 * 25 = 111112
Ergebnis: 31
1 0 1 1 1 1 1 0 0 1 0 1 0 1Vorzeichen der Mantisse negativ, daher ist die Zahl negativ
Mantisse: 1100101012
positiver Exponent: 1112 = 710
Zahl in normierter Gleitkommadarstellung: -0,1100101012 * 27 = 1100101,012
Ergebnis: -101,25
1 1 1 1 0 1 0 0 1 1 0 1 0 1beide Vorzeichen negativ, daher ist die Zahl negativ und der Exponent negativ
negative Mantisse: -1001101012
negativer Exponent, daher Zweierkomplement des Exponenten: 0102 = -210
Zahl in normierter Gleitkommadarstellung: -0,1001101012 * 2-2 = 0,001001101012
Ergebnis: -0.15087890625
(Vergleichen Sie das mit dem Ergebnis des Beispiels ganz oben!)
Zahlenbereich
Die Formel aus der Schulübung:Eingesetzt für B = 2 (Binärsystem), m = 10 (von ganz oben) und e = 4 (von ganz oben):
Labels: POS1-1
Abonnieren Kommentare [Atom]


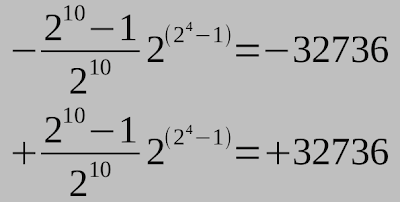
Kommentar veröffentlichen